자바의 정석 Chapter 2 - 진법

이번 장에서는 컴퓨터가 처리하는 데이터의 표현 방식에 대해서 설명하고자 한다.

3.1 10진법과 2진법

컴퓨터는 기본적으로 계산을 수행하는 장치이다.
따라서 컴퓨터가 처리하는 모든 데이터의 기본 단위는 숫자이며,
문자, 이미지, 소리 등 우리가 다루는 다양한 정보들도 결국은 숫자의 형태로 변환되어 처리된다.

여기서 말하는 ‘수(數)’란, 사물의 개수, 순서, 크기 등을 표현하고 측정하기 위한 인간의 추상적 개념이다.
수학적으로는 복잡한 공리 체계로 정의되기도 하지만,
컴퓨터나 프로그래밍에서 다루는 수는 우리가 초·중·고에서 배우는 수준의 개념만으로도 충분하다.

컴퓨터는 사용자의 목적에 따라 특정 데이터를 가공·처리하는데,
이때 사용되는 모든 데이터는 결국 숫자로 이루어져 있으며,
이 숫자들을 일관되게 표현하고 계산하기 위해 필요한 규칙이 바로 **‘진법’**이다.

---

🔹 진법과 위치값 기수법

**진법(進法)**이란 숫자를 표현하는 체계이며, 대부분의 진법은 **‘위치값 기수법’(positional numeral system)**에 기반을 둔다.

• 기수법은 수를 숫자로 표현하는 방법이고,
• 위치값 기수법은 숫자의 위치에 따라 그 수의 값이 결정되는 방식이다.

예를 들어 십진수 345는 다음과 같이 해석된다:

• 5는 일의 자리 → 5 × 10⁰ = 5
• 4는 십의 자리 → 4 × 10¹ = 40
• 3는 백의 자리 → 3 × 10² = 300

따라서 345는 300 + 40 + 5로 계산된다.
이처럼 각 자리마다 **위치에 해당하는 가중치(거듭제곱 값)**를 곱해 전체 수를 구성하는 방식이 위치값 기수법이다.

---

🔹 컴퓨터와 진법의 관계

초기의 컴퓨터인 **애니악(ENIAC)**은 10진법을 기반으로 설계되었지만,
컴퓨터는 전기적인 신호를 이용해 동작하는 장치다.

전류의 흐름이 있는 상태(ON)와 없는 상태(OFF)의 두 가지 상태만을 명확하게 구분할 수 있다.

따라서 컴퓨터 내부에서는 이진법(2진법), 즉 0과 1로 이루어진 숫자만 사용하는것이 전기적 특성과 가장 잘 맞고

회로 구성이나 오류 방지 측면에서도 더욱 간단하고 효율적하다.

이러한 이유로 현대의 모든 컴퓨터 시스템은 2진법을 기반으로 모든 데이터를 표현하고 연산한다.

🔹이진법과 자리수 개념 개요

• 이진법의 기본 구조
  • 2진법은 오직 0과 1만으로 데이터를 표현함
  • 표현 가능한 숫자 범위가 좁기 때문에, 같은 값을 나타내기 위해 더 많은 자리수가 필요

int의 크기가 32 byte라 32자리중 나머지값을 0으로 표현해야하지만 생략 함.

 

• 10진수와 자리수 비교
  • 예: 10진수 2는 2진수로 10 → 기본적으로 2자리 필요
  • 이는 10진수에서 9 + 1 = 10이 되어 자릿수가 증가하는 것과 동일한 원리
• 자리수 증가의 패턴 유사성
  • 10진수: 9 + 1 → 10 (1자리 → 2자리)
  • 2진수: 1 + 1 → 10, 11 + 1 → 100 (자리수 증가)
  • 이처럼 진법이 달라도 자리 증가 패턴은 동일하다.
  • 10진수는 0~9까지의 10개의 숫자로 표현이 불가능할 때, 자리수가 증가함.
  • 2진수는 0~1까지의 2개의 숫자로 표현이 불가능할 때, 자리수가 증가함.
• 핵심 이해 포인트
  • 이진법에서의 자리수 증가 원리는 10진수와 같은 논리 구조를 따름
  • 따라서 10진수의 자리수 개념을 떠올리면 이진수도 쉽게 이해할 수 있음

 

2진법과 10진법 덧셈 방식

 

자리수의 차이만 존재할 뿐, 세상 모든 숫자는 각 진법으로 모두 표현이 가능하다.

3.2 비트(bit)와 바이트(byte)

• 한 자리의 2진수를 컴퓨터에서는 비트라고 표현함.
• 1 비트는 컴퓨터가 값을 저장할 수 있는 최소 값
• 다만 1비트로 표현하기엔 너무 작은 단위라, 8개의 비트를 묶어서 바이트라는 단위로 정의.
• 1바이트는 컴퓨터가 표현할 수 있는 정보의 최소 단위이다.

비트와 바이트를 표현한 그림

• 이 외에, 워드(word)라는 단위는 CPU가 한번에 처리할 수 있는 데이터의 크기를 의미
• 기본적으로 4바이트에 해당하지만, CPU의 성능에 따라 바이트 수는 달라진다.
• 32비트 CPU에선 4바이트 / 64비트 CPU에선 8바이트
• 아래 이미지는 각 비트별 표현할 수 있는 값들을 표현한 그림이다

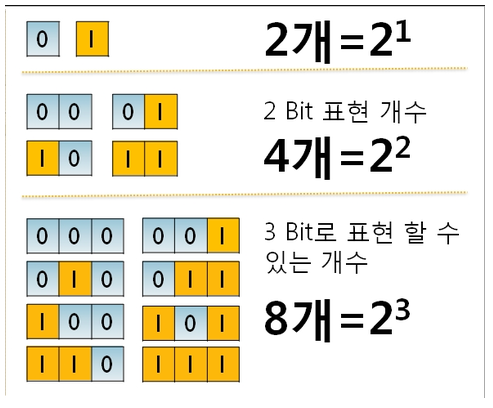
비트별 표현 가능한 데이터 개수

• 위 내용을 공식으로 표현하면 N비트로 표현할 수 있는 10진수의 공식은 아래와 같다.
• 값의 개수 : 2ⁿ
• 값의 개수 : 0 ~ 2ⁿ- 1

3.3 8진법과 16진법

• 2진법은 오직 0과 1로만 데이터를 표현하기 때문에, 자리수가 상당히 길어짐.
• 이를 보완하기 위해 8진법 16진법도 사용하는 경우가 많음.
• 8진수를 2진수 3자리를, 16진수는 2진수 4자리를 각 한자리로 표현하기에 자리수가 짧아진다는 장점이 있음.
• 또한 서로간의 변환도 간단함.

0부터 15까지의 값을 각 진법으로 표현한 도표

• 8진수는 8개의 숫자가 필요하기에 0~7까지 기호로 사용
• 16진수는 16개의 숫자가 필요하기에 0~9까지는 아라비아 숫자로 쓰고, 나머지 6개는 알파벳순으로 표현
• 예를들어 16진수 A는 십진수로 10이고, F는 15이다.

3.4 각 진수별 변환 방법

• 2진수, 8, 10, 16진수의 경우 결국 같은 의미의 숫자를 어떤 방식으로 표현할것인가를 나타내는 방법이다.
• 따라서, 각 진수별 변환도 가능하다. 설명하기 쉽게 X진수라고 표현하겠다.
• 위 진수의 핵심은 각 자리수가 의미하는 값, 즉 X값의 거듭제곱을 의미한다.
• 4자리 숫자라고 한다면, 맨 앞숫자부터 X의 3제곱, 2제곱,1제곱,0제곱을 의미한다.
• 10진수 또한 123이라고 한다면 (10의 2제곱 * 2) + (10의 1제곱 * 2) + (10의 0제곱 * 3)을 의미한다.
• 이진수의 111이라고 한다면 (2의 2제곱 *1) + (2의1제곱*1) + (2의 0제곱*1)이 되며, 7을 의미하게 된다.
• 위 방법으로 우선 값을 구하게 되면.. 기본적으로 10진수로 표현이 가능하다.
• 그렇게 구해진 값을 다시 X로 계속 나누어서 X에 해당하는 진법으로 변환이 가능하다.

진법 변경 방법의 경우 문장으로 적기에는 가독성이 떨어지고, 내 실력이 부족하다. ㅠㅠ

따라서, 설명이 잘 되어 있는 영상 2가지 참조하며, 생각날 때 한번씩 보겠다는 생각으로 영상을 공유한다.

 

3.5 실수의 진법 변환

진법 변황 참고 영상 :https://www.youtube.com/watch?v=fvNtkhhCrow 

 

 소수의 진법 변환 : https://www.youtube.com/watch?v=DwqqdTPldX4

 

음수의 진법 변환 :  https://www.youtube.com/watch?v=TvpBEXOMitE